Lie coalgebra
In mathematics a Lie coalgebra is the dual structure to a Lie algebra.
In finite dimensions, these are dual objects: the dual vector space to a Lie algebra naturally has the structure of a Lie coalgebra, and conversely.
Contents |
Definition
Let E be a vector space over a field k equipped with a linear mapping 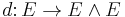 from E to the exterior product of E with itself. It is possible to extend d uniquely to a graded derivation[1] of degree 1 on the exterior algebra of E:
from E to the exterior product of E with itself. It is possible to extend d uniquely to a graded derivation[1] of degree 1 on the exterior algebra of E:
Then the pair (E, d) is said to be a Lie coalgebra if d2 = 0, i.e., if the graded components of the exterior algebra with derivation 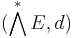 form a cochain complex:
form a cochain complex:
Relation to de Rham complex
Just as the exterior algebra (and tensor algebra) of vector fields on a manifold form a Lie algebra (over the base field K), the de Rham complex of differential forms on a manifold form a Lie coalgebra (over the base field K). Further, there is a pairing between vector fields and differential forms.
However, the situation is subtler: the Lie bracket is not linear over the algebra of smooth functions 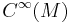 (the error is the Lie derivative), nor is the exterior derivative:
(the error is the Lie derivative), nor is the exterior derivative: 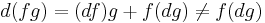 (it is a derivation, not linear over functions): they are not tensors. They are not linear over functions, but they behave in a consistent way, which is not captured simply by the notion of Lie algebra and Lie coalgebra.
(it is a derivation, not linear over functions): they are not tensors. They are not linear over functions, but they behave in a consistent way, which is not captured simply by the notion of Lie algebra and Lie coalgebra.
Further, in the de Rham complex, the derivation is not only defined for 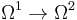 , but is also defined for
, but is also defined for 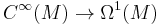 .
.
The Lie algebra on the dual
A Lie algebra structure on a vector space is a map ![[\cdot,\cdot]\colon \mathfrak{g}\times\mathfrak{g}\to\mathfrak{g}](/2012-wikipedia_en_all_nopic_01_2012/I/e949d4e54ff8079250d0f131c43ddd98.png) which is skew-symmetric, and satisfies the Jacobi identity. Equivalently, a map
which is skew-symmetric, and satisfies the Jacobi identity. Equivalently, a map ![[\cdot,\cdot]\colon
\mathfrak{g} \wedge \mathfrak{g} \to \mathfrak{g}](/2012-wikipedia_en_all_nopic_01_2012/I/d1ab2e8b5610c74b5435cbd442c24629.png) that satisfies the Jacobi identity.
that satisfies the Jacobi identity.
Dually, a Lie coalgebra structure on a vector space is a map 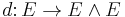 which satisfies the cocycle condition. The dual of the Lie bracket yields a map (the cocommutator)
which satisfies the cocycle condition. The dual of the Lie bracket yields a map (the cocommutator)
where the isomorphism 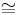 holds in finite dimension; dually for the dual of Lie comultiplication. In this context, the Jacobi identity corresponds to the cocycle condition.
holds in finite dimension; dually for the dual of Lie comultiplication. In this context, the Jacobi identity corresponds to the cocycle condition.
More explicitly, let E be a Lie coalgebra over a field of characteristic neither 2 nor 3. The dual space E* carries the structure of a bracket defined by
- α([x, y]) = dα(x∧y), for all α ∈ E and x,y ∈ E*.
We show that this endows E* with a Lie bracket. It suffices to check the Jacobi identity. For any x, y, z ∈ E* and α ∈ E,
where the latter step follows from the standard identification of the dual of a wedge product with the wedge product of the duals. Finally, this gives
Since d2 = 0, it follows that
![\alpha([[x, y], z] %2B [[y, z], x] %2B [[z, x], y]) = 0](/2012-wikipedia_en_all_nopic_01_2012/I/81d7ae1441ca0f4fd632dca64814a6a7.png) , for any α, x, y, and z.
, for any α, x, y, and z.
Thus, by the double-duality isomorphism (more precisely, by the double-duality monomorphism, since the vector space needs not be finite-dimensional), the Jacobi identity is satisfied.
In particular, note that this proof demonstrates that the cocycle condition d2 = 0 is in a sense dual to the Jacobi identity.
Notes
- ^ This means that, for any a, b ∈ E which are homogeneous elements,
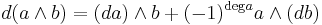 .
.
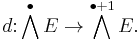
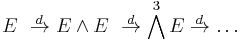
![[\cdot,\cdot]^*\colon \mathfrak{g}^* \to (\mathfrak{g} \wedge \mathfrak{g})^* \cong \mathfrak{g}^* \wedge \mathfrak{g}^*](/2012-wikipedia_en_all_nopic_01_2012/I/759209167cb7df7bf916b7f24fec68cc.png)
![d^2\alpha (x\wedge y\wedge z) = \frac{1}{3} d^2\alpha(x\wedge y\wedge z %2B y\wedge z\wedge x %2B z\wedge x\wedge y) = \frac{1}{3} \left(d\alpha([x, y]\wedge z) %2B d\alpha([y, z]\wedge x) %2Bd\alpha([z, x]\wedge y)\right),](/2012-wikipedia_en_all_nopic_01_2012/I/ba3f2f7a0595b224a461e33c25dfa43c.png)
![d^2\alpha (x\wedge y\wedge z) = \frac{1}{3} \left(\alpha([[x, y], z]) %2B \alpha([[y, z], x])%2B\alpha([[z, x], y])\right).](/2012-wikipedia_en_all_nopic_01_2012/I/1d44abf2bb96de234a7003e9c5a4bf81.png)